Can not get mole balance between mobile phase and solid adsorbed

Konstantin · June 6, 2022, 5:38pm

Hello!
Can someone explain how to get mole balance between mobile phase and solid adsorbed.
I run ‘GENERAL_RATE_MODEL’ with ‘MULTI_COMPONENT_LANGMUIR’ adsorption model with zero flow rate as I need to fit our experimental data and find par_diffusion coeffitiant - it all works well except that amount of mole of adsorbed component on solid part after 300 minutes and what is left in liquid part is not equal to amount I started with at time zero.
I pull out solution_bulk, solution_solid and solution_particle, please see below
model.root.input[‘return’].unit_000.write_solution_solid = 1
model.root.input[‘return’].unit_000.write_solution_particle =1
model.root.input[‘return’].unit_000.write_solution_bulk = 1

and I expect that
initial solution_bulk * solution volume = solution_bulk * solution volume + solution_particle * pore volume + solution_solid * solid volume,
but it is not.
Please let me know where I am wrong.
Please see my script below:

import numpy as np
import matplotlib.pyplot as plt

from cadet import Cadet
Cadet.cadet_path = ‘C:\Users\konstantin\Anaconda3\pkgs\cadet-4.3.0-hbe28382_2\bin’

total_time =300*60 #s
time_frame = 1000

does not metter as flow rate is zero

col_length = 0.01 # m
cross_section_area = 0.1 # m2

col_porosity = 0.8
par_porosity = 0.1
par_radius = 3.25E-04 #m

col_dispersion = 3.789E-06 #m2/s
film_diffusion = [6.034E-02] #m/s
par_diffusion = [1.62E-09*8,] # m2/s

mcl_ka = [10.58735191,] # it is Langmuir coefficient b, m3/mol
mcl_kd = [1,]
mcl_qmax = [22471.33561/mcl_ka[0],] #mol / m^3

#Case A
concentration_ini = 1 #initial concentration in the solution mol/m3
init_q = 0

const_coeff = [concentration_ini,] # concentration mol/m3
Q = 0 # Flow rate in m^3*s^-1

#Model
model = Cadet()
model.root.input.model.nunits = 3

#Inlet Model
model.root.input.model.unit_000.unit_type = ‘INLET’
model.root.input.model.unit_000.ncomp = 1
model.root.input.model.unit_000.inlet_type = ‘PIECEWISE_CUBIC_POLY’

#General Rate Model
model.root.input.model.unit_001.unit_type = ‘GENERAL_RATE_MODEL’
model.root.input.model.unit_001.ncomp = 1

Geometry

model.root.input.model.unit_001.col_length = col_length
model.root.input.model.unit_001.cross_section_area = cross_section_area # m^2,

#model.root.input.model.unit_001.velocity = 0.000204933 # m/s

model.root.input.model.unit_001.col_porosity = col_porosity # -
model.root.input.model.unit_001.par_porosity = par_porosity # -
model.root.input.model.unit_001.par_radius = par_radius # m

Transport

model.root.input.model.unit_001.col_dispersion = col_dispersion # m^2 / s (interstitial volume)
model.root.input.model.unit_001.film_diffusion = film_diffusion # m / s
model.root.input.model.unit_001.par_diffusion = par_diffusion # m^2 / s (mobile phase)
model.root.input.model.unit_001.par_surfdiffusion = [0.0,] # zero m^2 / s (solid phase)

Adsorption Model

model.root.input.model.unit_001.adsorption_model = ‘MULTI_COMPONENT_LANGMUIR’
model.root.input.model.unit_001.adsorption.is_kinetic = True
model.root.input.model.unit_001.adsorption.mcl_ka = mcl_ka # m^3 / (mol * s) (mobile phase)
model.root.input.model.unit_001.adsorption.mcl_kd = mcl_kd # 1 / s (desorption)
model.root.input.model.unit_001.adsorption.mcl_qmax = mcl_qmax # mol / m^3 (solid phase)

Initial Conditions

model.root.input.model.unit_001.init_c = [concentration_ini,]
model.root.input.model.unit_001.init_q = [init_q,]

#Setting up the Discretization

Grid cells

model.root.input.model.unit_001.discretization.ncol = 100
model.root.input.model.unit_001.discretization.npar = 6

Bound states

model.root.input.model.unit_001.discretization.nbound = [1]

Other options

model.root.input.model.unit_001.discretization.par_disc_type = ‘EQUIDISTANT_PAR’
model.root.input.model.unit_001.discretization.use_analytic_jacobian = 1
model.root.input.model.unit_001.discretization.reconstruction = ‘WENO’
model.root.input.model.unit_001.discretization.gs_type = 1
model.root.input.model.unit_001.discretization.max_krylov = 0
model.root.input.model.unit_001.discretization.max_restarts = 10
model.root.input.model.unit_001.discretization.schur_safety = 1.0e-8

model.root.input.model.unit_001.discretization.weno.boundary_model = 0
model.root.input.model.unit_001.discretization.weno.weno_eps = 1e-10
model.root.input.model.unit_001.discretization.weno.weno_order = 3

Outlet Model

model.root.input.model.unit_002.unit_type = ‘OUTLET’
model.root.input.model.unit_002.ncomp = 1

#Time Sections

model.root.input.solver.sections.nsec = 1
model.root.input.solver.sections.section_times = [0.0,total_time,] # s
model.root.input.solver.sections.section_continuity = []

model.root.input.model.unit_000.sec_000.const_coeff = const_coeff # mol / m^3
model.root.input.model.unit_000.sec_000.lin_coeff = [0.0,]
model.root.input.model.unit_000.sec_000.quad_coeff = [0.0,]
model.root.input.model.unit_000.sec_000.cube_coeff = [0.0,]

#System Connectivity
model.root.input.model.connections.nswitches = 1
model.root.input.model.connections.switch_000.section = 0
model.root.input.model.connections.switch_000.connections = [
0, 1, -1, -1, Q, # [unit_000, unit_001, all components, all components, Q/ m^3s^-1
1, 2, -1, -1, Q] # [unit_001, unit_002, all components, all components, Q/ m^3s^-1

#Setting Up the Simulator and Running the Simulation
model.root.input.model.solver.gs_type = 1
model.root.input.model.solver.max_krylov = 0
model.root.input.model.solver.max_restarts = 10
model.root.input.model.solver.schur_safety = 1e-8

Number of cores for parallel simulation

model.root.input.solver.nthreads = 1

Tolerances for the time integrator

model.root.input.solver.time_integrator.abstol = 1e-6
model.root.input.solver.time_integrator.algtol = 1e-10
model.root.input.solver.time_integrator.reltol = 1e-6
model.root.input.solver.time_integrator.init_step_size = 1e-6
model.root.input.solver.time_integrator.max_steps = 1000000

#Return data
model.root.input[‘return’].split_components_data = 0
model.root.input[‘return’].split_ports_data = 0
model.root.input[‘return’].unit_000.write_solution_bulk = 1
model.root.input[‘return’].unit_000.write_solution_inlet = 1
model.root.input[‘return’].unit_000.write_solution_outlet = 1
model.root.input[‘return’].unit_000.write_coordinates = 1
model.root.input[‘return’].unit_000.write_solution_solid = 1 # return concentration on solid mol/m3
model.root.input[‘return’].unit_000.write_solution_particle =1
model.root.input[‘return’].unit_000.write_solution_volume = 1

Copy settings to the other unit operations

model.root.input[‘return’].unit_001 = model.root.input[‘return’].unit_000
model.root.input[‘return’].unit_002 = model.root.input[‘return’].unit_000

Solution times

model.root.input.solver.user_solution_times = np.linspace(0, total_time, 1001)

exec(open(‘utils.py’).read())

run_simulation(model)

Plotting the Results

plt.figure()

time = model.root.output.solution.solution_times
c = model.root.output.solution.unit_001.solution_inlet
c_max = np.max(c)

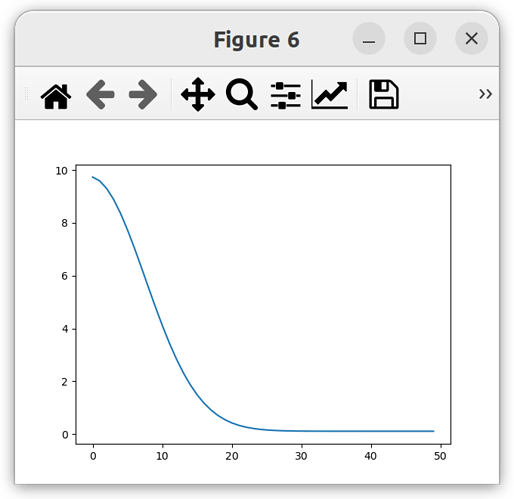
solution_solid = model.root.output.solution.unit_001.solution_solid[:, :, 0, 0]
solution_particle = model.root.output.solution.unit_001.solution_particle[:, :, 0, 0]
solution_volume = model.root.output.solution.unit_001.solution_volume

Thanks a lot!
Konstantin

lieres · June 8, 2022, 7:34am

Welcome Konstantin!

I assume you are working with batch uptake data. It is a valid apporach to use the GRM with zero flow rate in this case. You can also set column disprsion to zero. Column length and column radius do not matter then. Moreover, you need only one axial cell (ncol =1). If you are specifically interested in pore diffusion, I would refine the particle discretization instead (e.g. npar = 50).

The mass balance should work out when the porosities are correctly accounted for. The total mass is given by:

column_porosity * bulk_concentration + (1-column_porosity) * particle_porosity * pore_concentration + (1-column_porosity) * (1-particle_porosity) * adsorbed_concentration

Konstantin · June 8, 2022, 3:34pm

Lieres,
Thanks for the response!
I changed ncol to 1 and npar to 50, but I still got unrealistic amount of mole adsorbed on solids (almost ten times more), should I use solution_solid as adsorbed_concentration? Or it is somethin different? I have it defined like that:
solution_solid = model.root.output.solution.unit_001.solution_solid[:, :, 0, 0]

I also checked here: Output Group — CADET
that solution_solid has unit of mol/m3mp (but it is not mobile phase for sure if mp index stands for mobile phase).
Thanks again!

lieres · June 8, 2022, 4:46pm

You have actually found a bug in the documentation. It should read SP in the solution_solid group.

From the posted information I have no idea where the error migth be. Can you please send us executable code?

Konstantin · June 8, 2022, 5:20pm

Lieres,
Please, see my code uploaded, I run it in Spyder (Python 3.9) and CADET 4.3.0.
Stirring Tank for Cadet Forume 6-6-22.txt (6.8 KB)

Just in case, I use exec(open(‘utils.py’).read()) in the code to avoid “Accesses denied error” I got if I do it the way proposed in the introduction.
Thanks a lot!!!

j.schmoelder · June 21, 2022, 4:27pm

Hi Konstantin,

please excuse the silence, I was on a longer vacation.

Actually, the code seems to runs fine. I assume the issue is the following:

Your particles are rather large (1e-4 radius). So the molecules didn’t have enough time to migrate fully. This plot shows the solid concentration over the radial cells at the last time point. Note that the indices are (time, axial position, radial position, component). So here I just used the first axial cell and the first component:

plt.figure(); plt.plot(model.root.output.solution.unit_001.solution_solid[-1, 0, :, 0])

As you can see, the bead is not in equilibrium yet. So for your mass balance you would have to integrate over the sphere.

If you wait longer (here: 3000 min) and chose a smaller particle radius (here 1e-6 m) it becomes better.

If you now calculate the mass balance, things come out better.

m_{start} = c_{init} \cdot V_{fluid} = c_{init} \cdot \epsilon_t \cdot A_c \cdot L_c = 0.82

m_{end} = c_{bulk} \cdot \epsilon_{bed} + (1 - \epsilon_{bed}) \cdot \epsilon_{particle} \cdot c_{pore} + (1 - \epsilon_{bed}) \cdot (1 - \epsilon_{particle}) \cdot c_{solid} = 0.82

I hope this helps.

Konstantin · June 21, 2022, 7:19pm

j.schmoelder Hello!
That makes total sense!
I did not realize that I can pull out the solid concentration over the radial cells,
Thanks!!!
K

Konstantin · July 12, 2022, 6:19pm

Hello!
Can I also ask you how I can change the initial concentration of the bulk solution after some time (new test) in the code but keep solid and pore concentration profile from my previous test?
As before I have stirring tank with feed rate equals 0 but I want to change solution consecration with time using step function and I see that there is only option to do cubic polynomial on feed concertation but in my case it is always zero.
I tried to run independent consecutive tests but I can not set specific distribution on solid and pore concentrations among the particle radius, only an average.
I need instantly change the solution with fresh one (different bulk concentration), but keep the solids.
Thanks!
K

j.schmoelder · July 20, 2022, 6:58am

See here.