Structure of npartype and vol_frac

Chromatography Modeling
1

Hello,

I am looking into the spatial distribution of particles with different properties and their effect on adsorption columns.
For this I am using variations of size and porosity and their respective axial distribution inside the column.
My question is how npartype and the matrix for volume fractions are build.
Example:

model.root.input.model.unit_001.par_porosity = [0.33,0.5]             # -
model.root.input.model.unit_001.par_radius = [1e-6, 2e-6, 3e-6]             # m
model.root.input.model.unit_001.npartype = 6

In the documentation under “Ordering of multi dimensional data” the example given is

comp0bnd0, comp0bnd1, comp0bnd2, comp1bnd0, comp1bnd1, comp1bnd2.

In my case this could mean:

porosity0radius0, porosity0radius1, porosity0radius2, porosity1radius0, porosity1radius1, porosity1radius2.

or

radius0porosity0, radius0porosity1, radius0porosity2, radius1porosity0, radius1porosity1, radius1porosity2.

The order is relevant to know, because npartype is the column vector for the partype_volfrac Matrix.
Therefore the order of the columns need to be known to initialize this matrix.
The partype_volfrac Matrix in the example would look like one of these:

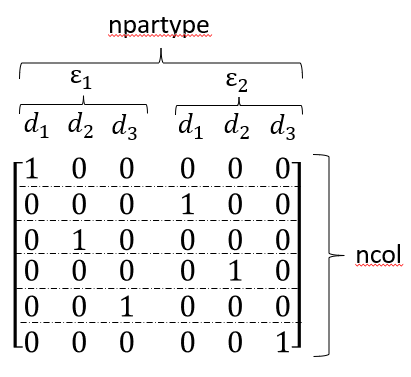
image
or
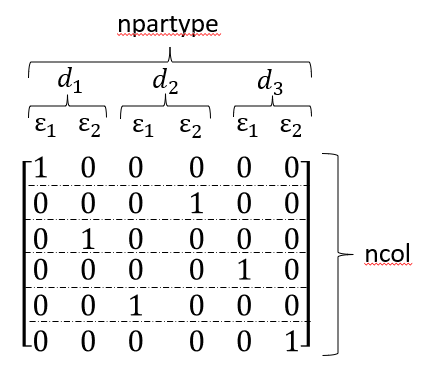
image

Hope someone can clarify which one of these 2 options is correct.

2

Hi Seemannsgarn,

from your example I suppose that you have 6 particle types given by two different porosities times three different particle radii, i.e.

model.root.input.model.unit_001.par_porosity = [0.33, 0.33, 0.33, 0.5, 0.5, 0.5]
model.root.input.model.unit_001.par_radius = [1e-6, 2e-6, 3e-6, 1e-6, 2e-6, 3e-6]
model.root.input.model.unit_001.npartype = 6

If you want to specify an axial distribution of these particle types, you need to specify PAR_TYPE_VOLFRAC for each particle type and axial position in an array with axial position major ordering. That is

model.root.input.model.unit_001.par_type_volfrac = [
    d_{type_0, col_0}, ..., d_{type_{npartypes-1}, col_0},
    d_{type_0, col_1}, ...,d_{type_{npartypes-1}, col_1},
    ..., ... , ...,
    d_{type_0, col_{ncol-1}}, ..., d_{type_{npartypes-1}, col_{ncol-1}}
]

Note that the sum of volume fractions at each axial position must always equal one, i.e.

\sum_{j=0}^{npartype-1} d_j|_x = 1 \quad \forall x, \text{ with } d_j \geq 0 \quad \forall j.

Hope this helps.

4 Likes