Thanks for the reply!
-
Disabling the consistent initialization unfortunately did not work. IDAS would fail at t=0, which is kind of strange since the
last_state_yandlast_state_ydotfrom simulation 1 should already be consistent? I think the problem may have something to do with thelast_state_yvector from simulation 1, it already contained some unreal values which I was not able to find at any t, r and z. -
Using external functions seems to be working. My test case is simple: GRM, Multi-component Langmuir
t \in (0, 4000): q_{max}=21, \; k_a=100
t \in (4000, 8000): q_{max}=23, \; k_a=110.A runnable Python code is below:
from cadet import Cadet
import numpy as np
import matplotlib.pyplot as plt
# replace the path
Cadet.cadet_path = r"C:\Users\zwend\CADET\cadetL2\bin\cadet-cli.exe"
## set up
c_feed = 0.0113
def create_model():
model = Cadet()
model.root.input.model.nunits = 3
model.root.input.model.unit_000.unit_type = 'INLET'
model.root.input.model.unit_000.ncomp = 1
model.root.input.model.unit_000.inlet_type = 'PIECEWISE_CUBIC_POLY'
model.root.input.model.unit_001.unit_type = 'GENERAL_RATE_MODEL'
model.root.input.model.unit_001.ncomp = 1
## Geometry
model.root.input.model.unit_001.col_length = 0.05 # m
model.root.input.model.unit_001.cross_section_area = 5.025e-6/0.05 # m^2
model.root.input.model.unit_001.col_porosity = 0.37 # 1
model.root.input.model.unit_001.par_porosity = 0.97 # 1
model.root.input.model.unit_001.par_radius = 0.045e-3 # m
## Transport
model.root.input.model.unit_001.col_dispersion = 2.061e-8 # m^2/s
model.root.input.model.unit_001.film_diffusion = [1.18e-5] # m/s
model.root.input.model.unit_001.par_diffusion = [0.8e-11,] # m^2/s [0.55e-11]
model.root.input.model.unit_001.par_surfdiffusion = [0.0, ]
## external adsorption isotherm
model.root.input.model.unit_001.adsorption_model = 'EXT_MULTI_COMPONENT_LANGMUIR'
model.root.input.model.unit_001.adsorption.extfun = 0
model.root.input.model.unit_001.adsorption.is_kinetic = 1
model.root.input.model.unit_001.adsorption.ext_mcl_ka = 100.0
model.root.input.model.unit_001.adsorption.ext_mcl_ka_t = 10.0
model.root.input.model.unit_001.adsorption.ext_mcl_ka_tt = 0
model.root.input.model.unit_001.adsorption.ext_mcl_ka_ttt = 0
model.root.input.model.unit_001.adsorption.ext_mcl_kd = 1.0 ## s^-1
model.root.input.model.unit_001.adsorption.ext_mcl_kd_t = 0
model.root.input.model.unit_001.adsorption.ext_mcl_kd_tt = 0
model.root.input.model.unit_001.adsorption.ext_mcl_kd_ttt = 0
model.root.input.model.unit_001.adsorption.ext_mcl_qmax = 21.0
model.root.input.model.unit_001.adsorption.ext_mcl_qmax_t = 2.0
model.root.input.model.unit_001.adsorption.ext_mcl_qmax_tt = 0
model.root.input.model.unit_001.adsorption.ext_mcl_qmax_ttt = 0
## external function
model.root.input.model.external.source_000.extfun_type = 'PIECEWISE_CUBIC_POLY'
model.root.input.model.external.source_000.section_times = [0.0, 4000.0, 8000.0]
model.root.input.model.external.source_000.velocity = 1e5 # set it to a large number
model.root.input.model.external.source_000.const_coeff = [0.0, 1.0]
model.root.input.model.external.source_000.lin_coeff = [0.0, 0.0]
model.root.input.model.external.source_000.quad_coeff = [0.0, 0.0]
model.root.input.model.external.source_000.cube_coeff = [0.0, 0.0]
## init condition
model.root.input.model.unit_001.init_c = [0.0, ]
model.root.input.model.unit_001.init_q = [0.0, ]
### Grid cells
model.root.input.model.unit_001.discretization.ncol = 50 ## increase as needed
model.root.input.model.unit_001.discretization.npar = 12 ## same as above
### Bound states
model.root.input.model.unit_001.discretization.nbound = [1, ]
### Other options
model.root.input.model.unit_001.discretization.par_disc_type = 'EQUIDISTANT_PAR'
model.root.input.model.unit_001.discretization.use_analytic_jacobian = 1
model.root.input.model.unit_001.discretization.reconstruction = 'WENO'
model.root.input.model.unit_001.discretization.gs_type = 1
model.root.input.model.unit_001.discretization.max_krylov = 0
model.root.input.model.unit_001.discretization.max_restarts = 10
model.root.input.model.unit_001.discretization.schur_safety = 1.0e-8
model.root.input.model.unit_001.discretization.weno.boundary_model = 0
model.root.input.model.unit_001.discretization.weno.weno_eps = 1e-10
model.root.input.model.unit_001.discretization.weno.weno_order = 2
model.root.input.model.unit_002.unit_type = 'OUTLET'
model.root.input.model.unit_002.ncomp = 1
model.root.input.solver.sections.nsec = 1
model.root.input.solver.sections.section_times = [0.0, 8000] # s
model.root.input.solver.sections.section_continuity = [0,0]
model.root.input.model.unit_000.sec_000.const_coeff = [c_feed] # mol / m^3; mg/ml = kg/m^3; 1 kda = 1 kg/mol 1.25/150
model.root.input.model.unit_000.sec_000.lin_coeff = [0.0]
model.root.input.model.unit_000.sec_000.quad_coeff = [0.0]
model.root.input.model.unit_000.sec_000.cube_coeff = [0.0]
model.root.input.model.connections.nswitches = 1
model.root.input.model.connections.switch_000.section = 0
model.root.input.model.connections.switch_000.connections = [
0, 1, -1, -1, 2.5 /(6e7),
1, 2, -1, -1, 2.5 /(6e7)]
model.root.input.model.solver.gs_type = 1
model.root.input.model.solver.max_krylov = 0
model.root.input.model.solver.max_restarts = 10
model.root.input.model.solver.schur_safety = 1e-8
# Number of cores for parallel simulation
model.root.input.solver.nthreads = 1
# Tolerances for the time integrator
model.root.input.solver.time_integrator.abstol = 1e-6
model.root.input.solver.time_integrator.algtol = 1e-10
model.root.input.solver.time_integrator.reltol = 1e-6
model.root.input.solver.time_integrator.init_step_size = 1e-6
model.root.input.solver.time_integrator.max_steps = 1000000
# Return data
model.root.input['return'].split_components_data = 1
model.root.input['return'].split_ports_data = 0
model.root.input['return'].unit_000.write_solution_outlet = 1
# Copy settings to the other unit operations
model.root.input['return'].unit_001 = model.root.input['return'].unit_000
model.root.input['return'].unit_002 = model.root.input['return'].unit_000
# Solution times
model.root.input.solver.user_solution_times = np.linspace(0, 8000, 1000+1)
return model
model = create_model()
model.filename = 'model.h5'
model.save()
data = model.run()
print(data)
model.load()
time = model.root.output.solution.solution_times
c = model.root.output.solution.unit_001.solution_outlet_comp_000 ## 1 mol/m^3 * 150 kg/mol=150 kg/m^3 = 150 mg/mL
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(time, c*150, c="orange")
ax.set_xlabel(r't/s')
ax.set_ylabel(r'conc./ mg/mL')
plt.show()
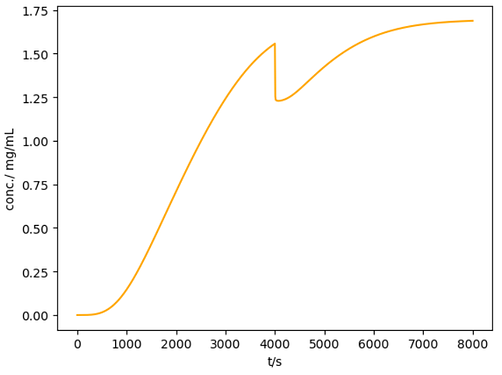
The warning would still appear: Warning: setExternalFunctions::113] Index 0 exceeds number of passed external functions (0), external dependence is ignored\r\n, but it should be fine. The following plot would appear:
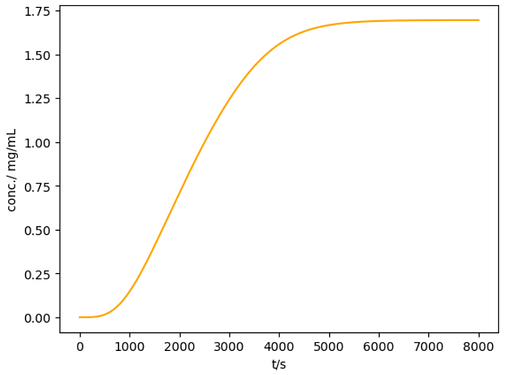
If there is no change in the isotherm parameters:
The sharp decrease at t=4000 made sense because q_{max} and k_a increased, the column continued to absorb the feed so the outlet concentration decreased.